Моделирование жидкости

Уравнение Навье Стокса — система дифференциальных уравнений в частных производных, описывающая движение вязкой ньютоновской жидкости. Уравнения Навье — Стокса являются одними из важнейших в гидродинамике и применяются в математическом моделировании многих природных явлений и технических задач. Названы по имени французского физика Навье, Анри и британского математика Джорджа Стокса. Система состоит из двух уравнений: * уравнения движения, * уравнения неразрывности. В векторном виде для несжимаемой жидкости они записываются следующим образом: :

$$

 

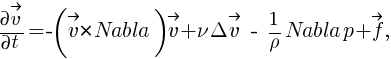
где 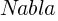— оператор набла(оператор Гамильтона),

$$ — оператор Лапласа,

$$

$$ — время,

$$

$$ — коэффициент кинематической вязкости,

$$

$$ — плотность,

$$

$$ — давление,

$$

$$ — векторное поле скоростей,

$$

$$ — векторное поле массовых сил.

$$

Неизвестные 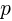и 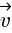являются функциями времени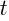

и координаты

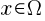, где 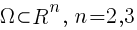— плоская или трёхмерная область, в которой движется жидкость. Обычно в систему уравнений Навье — Стокса добавляют краевые и начальные условия, например:

$$

 

 

 

Опубликовано в Наука, просмотров: 2 707, автор: Александр (0/1)